「3DCG の原理」による 3DCG プログラミング

「基本プログラム」 メニュー

※ いずれも JavaScript によるプログラムです。

※ 表は縦方向↑↓の順で見てください。


3DCG を自分の計算でプログラムしましょう

このホームページでは入門サイトのように順を追って丁寧に教えているわけではなく、「基本プログラム」と銘打ったサンプルファイルをいくつか用意しているだけ です。

しかし、難しい計算から解放されて、比較的楽にプログラミングを行うためのヒントになっているはずなので、難しい計算に挫折した方やこれから 3DCG プログラミ ング を勉強しようという方はどうぞ参考にしてください。

2019/5/26 私自身で基本プログラムを読み返して、ちょっとこれではわかりにくく、「読者がわからないまま、説明が先へ進んでいる」という教えの場としてあまり良くない形になっている気がしました。残念ながらすぐには直せないので警告だけお知らせしておきます。

「基本プログラム」は上のメニューからリンクをクリックしてください。

- このページのもくじ -

※2018/9/23以前まで、「基本プログラム」の一部で不備がありましたが、現在は修正済みです。


※たしか、2021/9/10 に行ったシステムの調整を境に、2023/6/4 までの1年9カ月ものあいだ、このページはサイトのどこからもリンクされずに隠れていましたが（存在はしていたと思う）、このたびページを正しく表示できるようにした上で、web6047 トップページからリンクを張りました。


3DCG プログラミングの習得ルートについて

以下のルートでの習得は難しいと思います。


 　 いきなり、ここから　→ 　 3DCG の一般的な計算を学ぶ
（行列など難しい数学）		 → 3DCG の技術を習得

しかし、以下のルートなら比較的楽に習得できると思います。

ここで紹介する簡単な計算
（小学５年生の割合の単元）		 → 3DCG の技術を習得
（3次元空間のりくつを学ぶ）		 → 3DCG の一般的な計算を学ぶ
（行列など難しい数学）		 → 3DCG の技術を習得


3DCGプログラミングには２つの壁があるように思います。

  1. １つは DirectX や OpenGL などを使って、行列計算したり内積や外積を駆使して三次元空間の座標を計算すること。つまり「難しい数学」。
  2. もう１つは、「３次元空間のりくつ」です。
    たとえば、何も知らなければ視点（0,0）の位置にモデルを配置してしまい、現実で言えば目玉と物体の中心が重なっているという状態になってしまいます（私がそれをやりました）。これは目で見るものが目から何 cm か離れているように、プログラムでも物体を視点から離さなくてはならないということです。ほかにも、
    物体が移動した後に物体を回転（自転）させようとすると、実は視点を中心に公転していたとか、
    物体が移動した後に物体を拡大しようとすると、視点から広がるように偏った拡大になってしまうなど、計算の順序にも最初は悩みます。

ここで紹介している 3DCG 計算は、とても簡単な計算式（小学校５年生程度の式）なので、上記１つめの「難しい数学」に取り組まなくても 3DCG プログラミングを楽しめます。

ただし、もう１つの壁、「３次元空間のりくつ」は避けて通れません。なんてったって、3DCG プログラミングですから３次元空間での事象は知っている必要があるでしょう。

しかし、１つめの壁（難しい数学）が除去されることで、「３次元空間のりくつ」に思考を集中できます。

簡単な計算式（小学校５年生程度の式）を使って「３次元空間のりくつ」を集中的に学んでから、3DCG の一般的な計算へ進むと習得がだいぶ楽になると思います。

私は最初のころは 3DCG の難しい行列にトライして苦しんでいましたが、この簡単な計算式でずいぶんとたくさんの 3DCG のプログラミングができたし、だいぶ 3次元空間のりくつについて学べたと思います。そして いろいろりくつを学んだ今なら、難しい行列を再度学んでもそんなに苦しまないと思います。でもこの簡単な計算式で事足りているので、難しい行列は必要なくなっています。

（なお、３次元空間の中で一歩進んだ高度な動きを実現したいという場合は、描画の部分で小学５年生の計算式を使っていても、動きの部分で難しい計算が必要になります）


「3DCG の原理」による計算はとても簡単

3DCG の一般的な計算は、ベクトルや内積、外積、行列計算に、難しいC言語のデータ型など、難しい言葉や難しい知識にあふれています。

しかし、3DCG の原理を見ると、とても簡単な計算式になっています。

h = x * ( s / z )、v = y * ( s / z )

これは、3次元空間の x, y, z に配置された点は 2次元の画面上の h, v という座標に対応するという計算式です。

Wikipedia の 3次元コンピュータグラフィックスの原理の項目に書いてあるものです。

https://ja.wikipedia.org/wiki/3次元コンピュータグラフィックス#原理

その項目で示されているりくつは、ちょっと理解するには難しい感じですが、どうも小学校 5年生くらいで習う「割合」の算数の知識だけで成り立っているように見えます。

このホームページ（上のメニューの基本プログラムの各プログラム）では行列計算を一切使わず、3DCG のライブラリやハードウェア（3DCG計算用のIC）も使わず、JavaScript によるソフトウェア計算と JavaScript でのコンピューターグラフィクスの出力先である CANVAS タグへの描画だけで 3DCG を描いています。


簡単な「3DCG の原理」で計算しても、難しいところがある

計算は前述のように四則演算なので結構簡単だと思いますが、それでも難しいところがあるので最初に挙げておきます。

■「3次元空間のりくつ」を理解するのが難しいです。

●視点と物体の座標は離さないと まともな画面にならない。

何も考えずに計算すると、視点と物体が重なった状態での描画を行ってしまうので、視点を原点として、物体を Z 方向に引き離した状態を描く必要があります。

●画面の縦座標と、3DCG の縦座標は上下が逆になっている。

そのままだと上下逆のモデルが描かれてしまいます。

●画面の原点は左上で、3DCG の原点は中央である。

そのままだと画面の左上を中心に描いてしまいます。

●目で見る景色には「焦点距離」というものがあり「50 で固定」とわかってしまえば悩みませんが、それを知らないあいだは、「焦点距離」をあれこれいじってしまい、悩むことがある。

上記で紹介した計算式の、

h = x * ( s / z )、v = y * ( s / z )

この s が焦点距離で、通常は 50 固定で大丈夫だと思います。

分かりやすく言うと、一時話題になった「ペットの鼻デカ写真集」のような画面を描きたいならこの値を 5 とかにします。

月や富士山など遠くにある物体を望遠したところを描きたいならこの値を 200 とかにします。

これはカメラのレンズが何 mm という話と同一です。

スナップ写真などを撮るための一般向けのカメラはこのレンズのサイズが 50 mm くらいになっていて、これは人間の目で見た景色と同じになることを想定した値だそうです。 3DCG で描く画面も人間の目で見た画面を描きたいはずなので基本的に 50 にします。

ただ、あえて調整したいときは 200 にしたりすることもあると思います。


どうして現実のレンズの 50 mm と、プログラムのピクセルが関与するはずの 50 という値が同じで一致し、それなりの画面が描けるのか、という疑問がわくと思い ます。

あまりうまく説明できませんが、割合の計算なので単位は mm でもピクセルでも出来上がる結果は同じ、、ということだと思います。

以下は 3DCG の原理の式の縦座標の計算を例にして、単位が何であっても同じこと、を示しています。

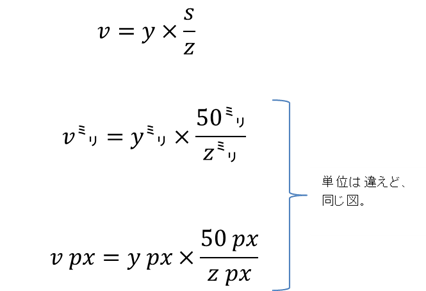
（ちょっと難しいかもしれませんが、ニコンの「焦点距離」の説明のページ ）

●それに加えて、「2D 画面の引き伸ばし」というのも必要です。

いろいろ言うと難しく感じてしまうかもしれません。私もだいぶ悩みました。

「計算結果の 2D 座標 h, v をそれぞれ 14 倍くらいする」

とわかっていればいいので すが、そういう知識はネット上にあまり見かけません。

つまり、上記の計算式 h = x * ( s / z )、v = y * ( s / z ) で 2D 座標 h, v を算出したら 14 倍しないと画像が小さいんです。

これはネガフィルムの画像を印画紙に拡大して焼き付ける工程と同じことなんじゃないかと思います。

ほかに、目で見る景色が目玉の網膜に写る際も、網膜に照射される景色は小さいと思いますが、頭で視界が処理されるとだいぶ大きく見えていますよね。

焦点距離の値を理解していないために でたらめな焦点距離にしていて、なおかつ、この拡大率も小さいままの状態で、「景色がおかしい」と言って試行錯誤しているあいだというのは、だいぶ苦しかったです。

拡大率を上げないままで焦点距離をいじっているだけではまともな画面には まず ならないんです。

14 倍（実際に使っている値は14.25倍）という値はどこから出てきたかというと、JavaScript でこの計算式で作成した 3DCG の景色画像と、 Shade3D で 同じ設定のシーンを作って作成した 3DCG の景色画像が一致する倍率を手作業で ずらしずらし で探った結果が 14.25 だったんです。

●視点が動くときは、物体は逆方向に動きます。

みなさんが顔を右に動かしたとき、見える景色は顔の動きの方向と逆方向（左）に動いていますよね。

視点を動かしたいと思ったら、「視点が動く」のではなく「物体が逆方向に動く」というりくつで計算します。

●回転する場合、どんなタイミングでその計算をするのか。

たとえば「3D モデルのデータ」に対して回転計算すると、モデルがモデルの中心を中心にして回転します。

対して、3D モデルを 3次元空間の指定の場所に移動してからその座標について回転計算すると視点（視点が３次元空間の原点なので）を中心にモデルが回転します。

そのへんのちがいもわかるまで難しいです。

（物体が自転するのか、物体が視点を中心に公転するのかという違いです）


変なタイミングで変な計算をしていると、画面がまともにならず、その原因がなかなかわからず非常に悩みます。

Excel を使って同じ計算を表で一望して、座標の動きを追跡する…なんてこともやりました。

私は平凡な脳みそを努力で動かしているタイプの人なので、それでもできずに敗退して朝方にやりたいことができないままに寝床に入るときは屈辱感を味わったり、悲しくなったりもします。

難しいですが、慣れてわかるようになると、思い通りにあれこれできるようになりそれが結構楽しいので、ぜひ くじけずに頑張ってほしいと思います。

●回転させるには sin と cos の三角関数（高校数学）を使う必要があります。

回転をしない 3次元空間の描写は

h = x * ( s / z )、v = y * ( s / z )

で計算できるので、小学校５年生の知識でいけると個人的に思っていますが、回転させる場合は三角関数が必要になります。

３次元空間上の x, y, z を三角関数で回転させてから、上記の式を使って 2D 画面へ描写する、という手順になります。

３次元空間上の x, y, z を三角関数で回転させる　とは：

いったいどうやるのかと思いますが、実は 3次元空間の中で、x, y, z のうち、x, y だけに注目するとそれは２次元の平面です。

x, y 平面（横方向、高さ方向）なので、目の前で指先で大きく丸を描くような回転になります。

また、x, y, z のうち、x, z だけに注目するとそれも２次元の平面です。

x, z 平面（横方向、奥行き）なので、地上をぐるっと回るような回転になります。

そういうわけで３次元空間の中で回転と言っても、実は２次元座標系を想定して回転しています。

２次元での回転：

３次元空間の中で２次元座標系を想定して回転するということですが、では２次元の回転とはどういうことでしょうか。

回転は sin, cos を使いますが、結構理解は難しいですよね。というより教える側のほうで「説明をすることが難しい」のかもしれません。


●光の加減を計算するところでは内積をちょっと使っています。また、面が向いている向き（法線という）を得るために外積をちょっと使っています。

「ちょっと使ってる」というのは、「内積、外積が何なのかについての理解を省略して、公式を使うだけでよい」というのと「その公式は簡単な四則演算である」ということから来てい ます。

ちょっと使うのは簡単ですが、理解するのは難しく時間がかかります（高校の幾何学（キカガク）という分野の数学です。私も理解は省略したままです）。


■プログラミングが難しいです。

3DCG の計算は h = x * ( s / z )、v = y * ( s / z ) を使えばいいので簡単だと思いますが、プログラムをどうやって組むのか、という部分がだいぶ難しいと思います。

●x, y, z という3次元座標の集合体である 3D モデルをどんなデータ形式にしてプログラムするか。

特に決まったフォーマットがあるわけではないので、自分次第です。

[ x, y, z ] のような配列でもいいし、{ x : 0, y : 0, z : 0 } のようなオブジェクトでもいいんです。

（配列とオブジェクトとどちらが処理が速いかは、大きな差はないみたいですが配列のほうが多少速いようです）

●このホームページの上のメニューに表示されている「canvas - 8（陰影付け）.html」の draw() 関数を見てもらうと分かりますが、まるで素材をいろいろな方法で粘土みたいに こねていくような、料理するような、いろいろな工程を経て描画に至る、みたいなプログラムになっています。

計算式は h = x * ( s / z )、v = y * ( s / z ) で単純でも、回転させて２種類の陰面消去を行って、色に光の加減を付けて…といろいろやろうとすると、少し大掛かりなプログラムになってしまいます。

しかしそれでも、「canvas - 2（線を描画）.html」を見るとワイヤーフレームの時点では割とシンプルなプログラムでわかりやすいし、そもそもちまたの行列計算や内積、外積、ベクトルに視錐台の理解など、そういう難しいものをやらずに済むので、だいぶわかりやすい環境で 3DCG プログラミングができると言えます。

●うまくいかない場合、そのデバッグが難しいです。

どうしてうまくいかないのか、とデバッグするのは、3DCG の場合、とりわけ難しいです。

３次元空間の動きが、ほんとにどうしてもうまくいかないとき、解決の手段として

「１から筋道立てた数学（図形）の計算を考える」

という方法があります。

適当にやってうまくいかないときは、そういう筋道立てたやり方に切り替える必要があります。

x, y, z の座標の動きを見ていく、という方法もありますがそれも難しいです。


以上、いろいろ難しい難しいと繰り返しましたが、「基本プログラム」と銘打って、順を追ってサンプルファイル（ページの上のメニュー）を用意したので参考にしてください。

私の苦労と根気の結晶ですが、著作権などは特に考えず、自由に使ってください。

コピーを取って自分のプログラムに使ったり、いろいろやってもらって大丈夫ですので。


「3DCG の原理」で計算した場合のクオリティ

出来上がる 2D 画面のクオリティの可否について簡単に挙げておきます。大切なことですね。

『簡単な式でできると言うけど、それで描かれる 3DCG と、「MAYA」とか「Blender」が描く 3DCG とは大きく異なるものになるんじゃないか…』

という疑問を払しょくしたいと思います。

クオリティ：◎　構図が市販ソフトと同じになる

市販の 3DCG レンダリングソフトと同じ構図を得られます。

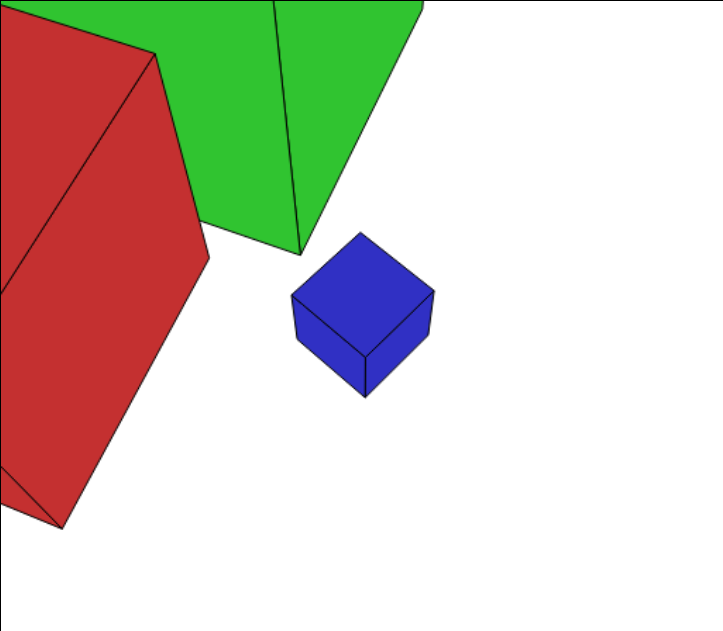
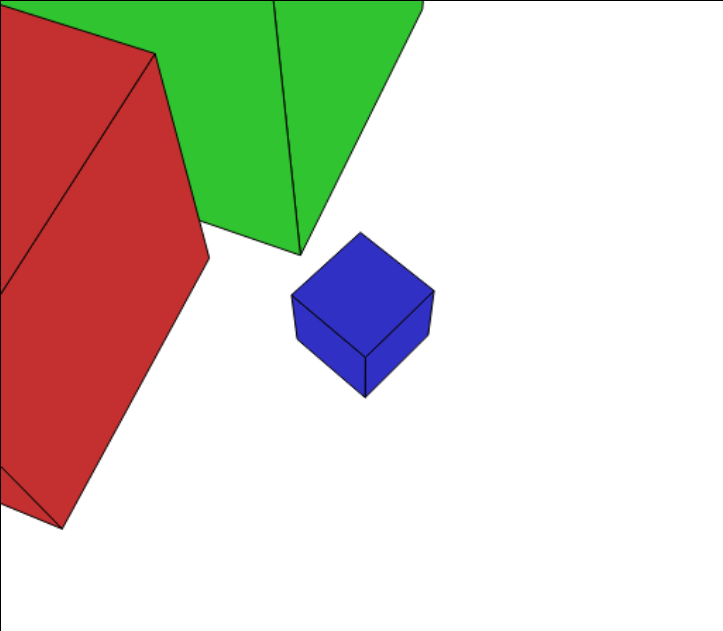
その実証として、市販の 3DCG レンダリングソフトである「Shade3D」（左）と JavaScript（右）とで下図のように同じ３次元の景観を作成します。（JavaScript のほうはもちろん、「3DCG の原理」を使ったプログラムです）


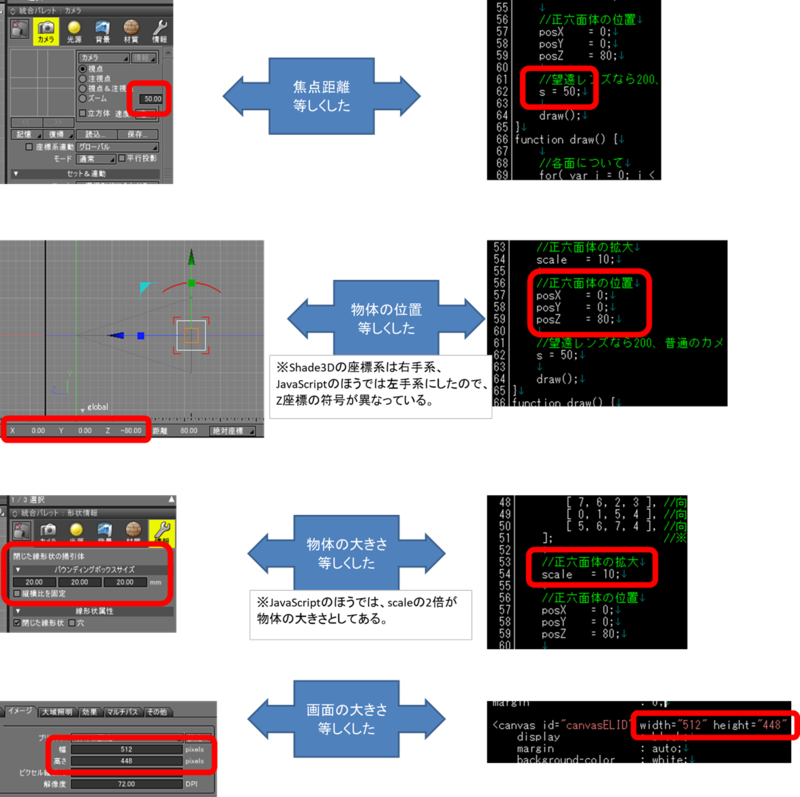
設定するものはこれで全部かなと思います。

そしてそれぞれレンダリングしたところです。

Shade3D作
 JavaScript作

どちらも大きさや遠近感の様子が同じになっています。GIF アニメで重ねて確認

そういうわけで構図については特に NG な点はないと思います。

 クオリティ：○　陰面消去されている

「3DCG の原理」の計算に、「画家のアルゴリズム」と「法線ベクトル法」という２つの陰面消去法を加えた場合の話ですが、上のメニューに並べている「基本プログラム」では「奥に隠れて見えないはずの面」をちゃんと消去しています。

しかし、簡易的な方法なので、２つの物体が重なったときなど、表示がおかしくなる場合があります。

クオリティ：○　陰影がある

これも「3DCG の原理」の計算に別途計算を加えた場合の話ですが、上のメニューの「基本プログラム」では「ランバート反射」という計算を使って、明るい面は明るく、暗い面は暗く、という陰影をつけています。

計算の調整次第では市販ソフトの「簡易レンダリング」程度には近づけることができます。

（「3DCG の原理」により とてもシンプルに 3DCG を描画できるので、「陰面消去」や「陰影」などのその他の計算にプログラミングの力を注ぎやすい…と言えます）

クオリティ：×　テクスチャがない

画像を面に張り付けるといった、「テクスチャマッピング」は処理速度の関係でできません。

ただ、静止画をレンダリングしたいだけなら、可能かもしれません。

３次元空間で面をマス目状に分割し、そこにビットマップをピクセル単位で描くという方法があります。（その例）

クオリティ：×　処理速度が遅い

すべてソフトウェアによる計算なので、ちょっと面（ポリゴン）の数が増えると処理が遅くなります。

ごく簡単なゲームや、ホームページ上のオブジェ（飾り）の作成程度には使えると思います。


補足

■補足：　「可能である」と分かっていて「基本プログラム」にまだ盛り込んでいないもの：

●補足：　テクスチャの代わりとして、CANVAS のパス描画を３次元空間に描くことができます。

人型のモデルを作ったとして、顔がないと寂しいでしょう。 

3DCG で顔を描くことを初めて考えるときは、ポリゴンによるデコボコを駆使して凹凸（おうとつ）によって目を表現したり、口を表現したりしようとしますが、それは非常に難しいことです。

テクスチャ（画像）を貼って表現するほうが現実的です。

しかし、グラフィックチップ（IC）などハードウェアを使わずにソフトウェア計算だけでテクスチャを実現するのはとても重い処理になってしまい、これもまた難しいです。

ここで、幸運なことに JavaScript の CANVAS の「パス」機能で顔を描き、３次元空間内に配置することができます。

下図は JavaScript の CANVAS のパス機能で描いた図です。

There is no canvas.

このパスは直線だけで構成されています。

パスには arc() など曲線を描く機能もありますが、３次元空間で曲線を描くのは困難なので直線だけを使います。

（2023年6月4日追記：ベジェ曲線は3次元空間上に配置可能です。ここで説明しています）

また、あまり細かいパスだと描画に時間がかかると思うので、なるべく単純な絵にしたほうが良いと思います。

上図の顔をクリックすると、パスを作ったときの元の絵を表示します。

青い絵は Excel のドロー機能で描いた絵で、この絵を下に敷いて座標を探りながら x, y のパスのデータを作りました。


There is no canvas.

パスは x, y の２次元の座標で構成されていますが、データとして z 座標を加えれば、他のモデルと同様に３次元空間内で位置を移動したり回転させることができます。

この「z 座標を加える」というのはたとえば直線の　100, 100 ～ 200, 200　というパスだったら、 100, 100, 100 ～ 200, 200, 100　という感じで、とりあえず同じ値で z 座標を加えます。（z 座標を加えるのは、あくまでも３次元空間上の話で、２次元画面上では h, v に変換されます）

これを、h = x * ( s / z )、v = y * ( s / z ) の式を使って 3DCG の計算を行い、２次元座標 h, v にします。

そして、

cc.beginPath();
cc.moveTo( h, v );
cc.lineTo( h2, v2 );
cc.stroke();

のようにして描きます。（※ cc は CANVAS コンテキスト）

…というより、もともとここで紹介している 3DCG のプログラムは１つの面（四角形）を描くためにすでにパス機能を使っているので、それが「四角形」ではなく「ちょっと複雑な線」になっただけの話です。

だからパスの 3D の描画処理もほぼ同一の計算になります。

ちょっとわかりにくいですが、これについてのプログラムリストを掲載しておきます。

パス描画だけのプログラムリスト（※ちょっと特殊な記述の JavaScript プログラムになっています）

パスを 3D に表示しているプログラムリスト（※ちょっと特殊な記述の JavaScript プログラムになっています）


●補足：　地面に落とす影も、まだ試したことはありませんが、できるんじゃないかと思います。

３次元空間で光源と物体の頂点を結ぶ直線の延長線を地面に向かって伸ばし地面との交点を得る。これをすべての頂点で算出し黒で面を描けば地面に落ちた影になる と思います。

それが処理速度としてネックになるなら、光源と物体の中心との直線の延長線を地面へ伸ばし地面との交点を中心に、物体の大きさに合わせて、黒い円を描けば、簡易的な影として使えるのでは？と思います。


●補足：　光沢（スペキュラ反射）というものがあり、以前どこかのサイト（https://wgld.org/d/webgl/w023.html）で紹介されていた計算式でやってみたら わりと楽にできたので、プログラムに盛り込むことができると思います。

ただし、魅力的な計算ではありますが、この計算結果を効果的に表すには面（ポリゴン）の細かさが必要です。

光の輝きを複数の面を使って段階的に表すので、正六面体などの分割の粗い立体では１面を白く塗って（極端に言って1段階で）「光沢です」といった結果になってしまいます。

球体のような細かい分割を行わないとまともに表現できません。


■補足：　「3DCG の原理」で 3DCG を描くことを ”レンダリング” と言って良いのか

「レンダリング」とは、「画像や画面の内容を指示するデータの集まり(数値や数式のパラメータ、描画ルールを記述したものなど)を、コンピュータプログラムで処理し、具体的な画素の集合を得ること」です。（http://e-words.jp/w/レンダリング.html）

以上で紹介した内容は、「３次元データ（簡単な正六面体など）を、プログラムで処理して、2D 画面を得ている」ので、まさに「3DCG・レンダリング・プログラム」と言えます。

しかし、一般的に「レンダリング」と言ったら、もっと専門的な部類を指す気がします。

「レンダリング プログラムを作った」

と言った場合、人々は

「光の粒子の動きを自分で計算（レイトレーシング）して 2D 画面を得る」というようなプログラムを連想することが多いと思うんです。

そのため、このページで紹介した「3DCG の原理で 3DCG を描くプログラム」は、「レンダリング プログラム」とは言いにくいかもしれません。


おまけ

「サブディビジョン・サーフェス／ドゥ・サビン」

JavaScript 実行ページを開く

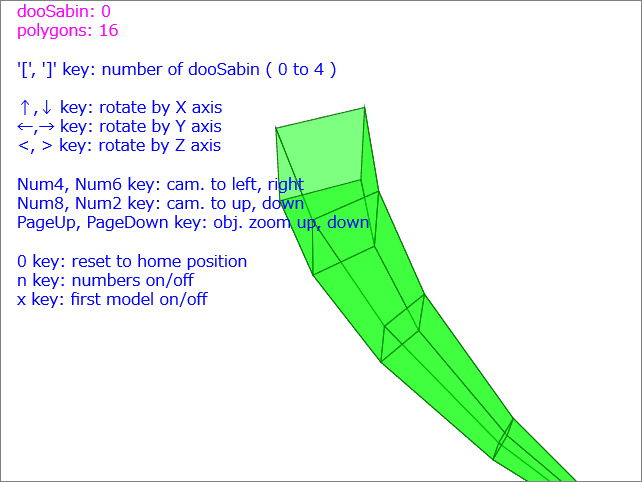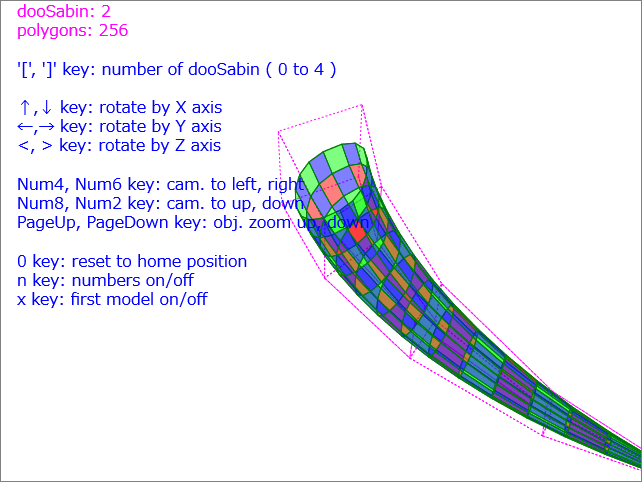今回のこの「3DCG の原理による 3DCG プログラミング」で紹介した「3DCG の原理の計算」を基本として、フレームワーク等をいっさい使わずに「サブディビジョン・サーフェス」を実装した例です。

「サブディビジョン・サーフェス」とは、「ごく簡単な形状を、分割を繰り返すことで滑らかな曲面へ変更する」というものです。

簡単なモデルから人の肌のような滑らかな曲面を作成できるので、現代の 3DCG にはなくてはならない技術と言えます。

▼Shade3D ではサブディビジョン・サーフェスを３種類から選べる。

同じサブディビジョン・サーフェスの仲間としては、3DCG アニメ映画の「トイストーリー」で有名な PIXER 社が開発した「OpenSubDiv」が有名です。

上記のプログラムはこの「ドゥ・サビン」の説明ページを参考にして作成しました。

DOO-SABIN SURFACES（英語）（サイト消滅したのでインターネットアーカイブを使用しています）

繰り返しになりますが、行列や視錘台などの難しい 3DCG の計算に労力を削られている状態では、このような技術の実現は遠かったと思います。


サブディビジョンサーフェス（リンクはWikipedia）


おわり


[by siteprogram2]