ベジェ曲線は3次元空間上に配置可能
ベジェ曲線の3D回転です。(JavaScriptのCANVASの2Dパス描画機能を使用)
感じの良いイラストが景気よく回転しております。
CANVAS には 2D パス描画の機能として、beginPath(), moveTo(), lineTo() などがありますが、さらに bezierCurveTo() (ベジェ・カーブ・トゥー)という関数もあります。bezierCurveTo() も含めて CANVAS にある描画メソッドはすべて2D描画用です。
moveTo() や lineTo() だけだと直線の組み合わせでカクカクとした絵しか描けませんが、bezierCurveTo() を使うと曲線が描けます。
bezierCurveTo() の説明:
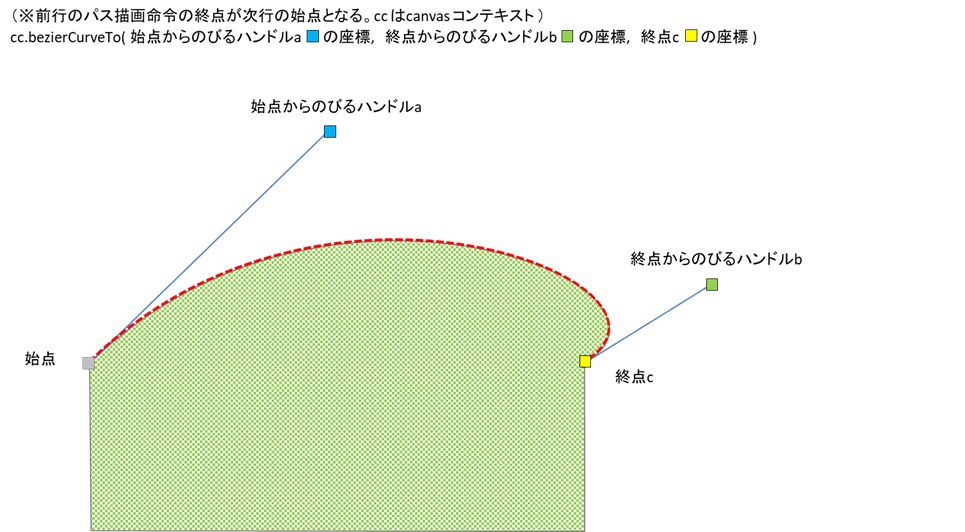
ハンドルの座標を変えることで、自由な曲線を描くというものです。
Excel や Word の図形や、Adobe イラストレーターの描画方法と同じものです。
ベジェ曲線の3D回転プログラムの簡単な例:
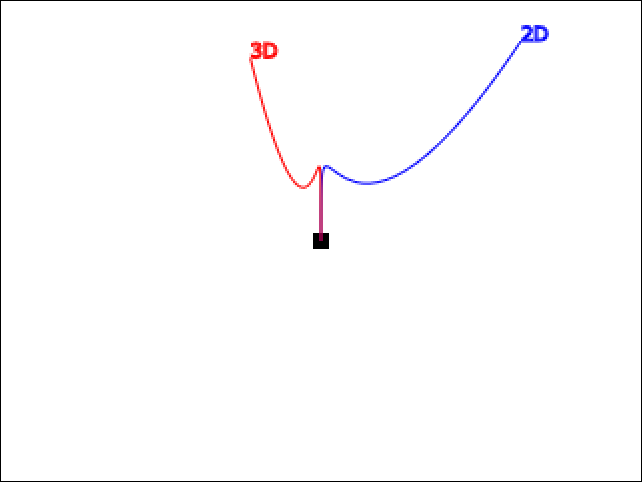
今まで「ベジェ曲線の3D回転は無理」だと思って私は直線による 3D 回転だけを行ってきましたが、実は bezierCurveTo() に渡す座標を単純に3D 回転すれば、(厳密には完全な 3D ではないのでわずかにゆがみますが)回転できるみたいです。
「完全な 3D ではない」というのは、bezierCurveTo() の引数の座標を 3D 回転しても、2D 描画のメソッドである bezierCurveTo() の内部のアルゴリズムでは当然、基本的に 2D の計算をしているのであって、3D の奥行きが考慮されていないんです。
とはいえ下記のサンプルを見てもらうとわかりますが、ほとんど 3D が表現できているので使える手法ではないかと思います。
(ただし、のちのち、もっと複雑なイラストを描いた際、うまくいかないこともあるかもしれません。今はまだ私も検証している段階です)
それから、もともと2DのデータだったものにZ座標を同じ値で追加することで、3次元空間に平面でパスを配置していますが、Z座標を同じ値ではなく異なる値を与えて、奥行きのある立体的なパスにする、というのも考えられます。Z座標をそれぞれ変えるだけなので試すのは簡単ですが、そういう立体的なパスはあまり用途がないと思うので、あまり試す気になりません。
サンプル実行 (下図のような JavaScript を実行します)

|

Webプログラマーも
びっくり! |
プログラムはわかりやすく書こうとしましたが、たぶん考えているとこんぐらがってくると思います。3D計算って経験が浅いと混乱するんです。
最後のrotate()関数は、高校数学の三角関数です。小中学生にとっては知らない内容の計算です。高校に入ったらこういう楽しい計算を授業で習うと思うので、楽しみにすると良いんじゃないかと思います。「そんなこと言ったって自分は勉強できないから」という人は、たぶん基礎でつまづいているので、基礎に戻って勉強するしかないんじゃないかと思います。勉強は、わからなかったものがわかったとき面白い、というものです。ですが、遊びやすい環境にいれば遊んでしまうし、逆に勉強しやすい環境にいれば自然と勉強することができます。要点がわかっていてほめるのが上手な誰か(よい先生)に出会って教えてもらえる、という「運」も必要かもしれません。勉強できる環境と、教えてくれる人。なかなか難しいですねぇ…。
勉強のしかた1: 自分の取り組みに関連させる
勉強の仕方は「勉強 苦手 方法」(リンクはBingで検索)などで Web 検索すれば、誰かが本当にいい方法を丁寧に教えてくれていると思うので、そちらを見てもらうのが良いかもしれません。
私も、DRAM回路の自作でコンデンサやトランジスタを使っているうちに、それまでほとんど勉強しなかったコンデンサやトランジスタを「ちょっと勉強したい」と思うようになりました。”学校のカリキュラムにあるから勉強をする” のに対して、”自分の取り組みで必要になったから勉強をする” というのは、勉強のエンジンとしては強力だと思います。とはいえ、実に広い電気という世界の、たった2つのコンデンサとトランジスタです。そこだけ勉強しても学校のカリキュラムをすべてクリアーできるわけもなく電気の資格が取れるわけでもありません。エンジンがかかるからと言って、学校の全カリキュラム1つ1つについて自分の取り組みを用意する…。なんてことは無理でしょう。
でもまぁ、エンジンをかけるにはもってこいの方法です。たった2つのことをまずは勉強してみて、それを皮切りに他の勉強もサクサク進むようになる…というのも十分あり得ます。
DRAMをやっているからコンデンサやトランジスタを好きになる。3DCGをやっているからsin, cosが好きになる。
何かに取り組むとオマケみたいに勉強へのエンジンが付いてきます。
勉強のしかた2: ふと思った疑問をメモして、自分で調べて回答する
誰でもやっている当たり前のやり方で勉強するのも無難な手ですが、ちょっと工夫してみると良いかもしれません。
たとえば勉強しているときに、ふと疑問に思ったことをどこかにメモしておくんです。
たとえば「三角関数の三角って何?」とか「方程式の方程って何のこと?」、それから「割り算の記号の÷って分数を絵にした状態?」、「素因数分解は少数には使えず、整数のみに使えるものなのかな?yes/no」。
そういう自分自身の内から発せられた疑問というのは、ほかでもない自分自身から出発した疑問です。学校の問題は学校のカリキュラムから出発したもので自分発ではないです。自分自身の動機というのは先ほども書いたようにエンジンとしては強力です。学校に勉強させられているのではなく、あなた自身が知りたがっているのですから。
疑問をメモしたら、その時でも、後でも良いので、時間のある時に回答をインターネットなどで探します。答えがわかったら、メモの横に答えを書いておきます。あとから読みたくなることもあるでしょうから。
- 「三角関数の三角って何?」
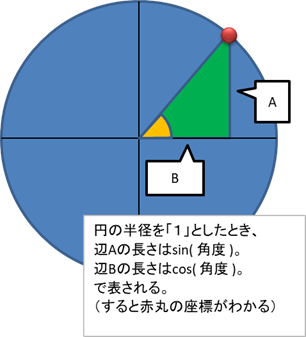
どうも何かを測量するのに、三角形を用いるのが都合が良いらしい。調べてみると とにかく昔から三角形を使っていた!
ちなみにこの緑の部分の三角形のことを言う。
- 「方程式の方程って何のこと?」
中国の言葉で、「算書九章算術にある言葉で、連立一次方程式を解く計算技術の名前」だそうだ。
日本語ではないので直感的な意味はなかなか見つからない。
- 「割り算の記号の÷って分数を絵にしたもの?」
÷はもともとは「半分」を意味する記号だったとか。「10÷」で「5」を意味する。https://99bako.com/1851.htmlより
記号の形が意味するのは、”物を2つに分ける” ということ?
また、Wikipediaで「÷」を検索すると、「分数表記を抽象化し、横棒と、その上下の分子と分母それぞれを点で表したものが元となっているといわれている」とも書かれている。
- 「素因数分解は少数には使えず、整数のみに使えるものなのかな?yes/no」
Wikipedia の「素因数分解」のページの1行目で、「ある正の整数を素数の積の形で表すことである。」と書かれている。yes。
こうやって調べていくと目の前の障害物(疑問)がなくなり、気持ちが満たされます。
勉強はしたくない!と言っているあなたなら、自分の気持ちに沿うというのは良いやり方なんじゃないかな。
ただあまり学校の勉強のテストの点数に関係のないことに時間をかけすぎると、学力も下がるので、できれば上記の赤く示した項目のように「どういう場合に使うのか」など知識が向上するようなものを調べるのが良いです。
ちょっと難しいですが実際の私のメモを1つ掲載すると、、
応用情報/整数の範囲で32767から-32768という場合どうして負のほうが大きいか
こういう微妙な疑問が解消されると、気持ちがすっきりして、これについては「範囲の数字」を受け入れることができます。
このやり方は人を選ぶので、自分はちがうなと思ったら忘れてください。