web6047 - 2026年 3月
ここは個人の趣味のページです。
昭和49年生まれ、血液型B型、男。
名前は、かわ、kawa、d_kawakawa、cookiepuddingman、平行四辺形 などいろいろあります。
工場で働いており、モノ作りが好きで小学生のころからプログラミングをやっています。
文書を書くときの助詞や助動詞、副詞などが苦手で、記事を書いて後から「不自然だな」と思ったりします。
注: ここに表示される氏名、名称と当ホームページはなんら関係ございません.
私がプログラミングを好むのは、プログラミングは私の「物づくり」に対する探求心と創造性を十分に満たしてくれるから、、です。
- 探求心:
1986 年 5 月末に発売されたファミコン版「ドラゴンクエスト」に衝撃を受け、憧れて、そのための断片的なプログラムをパソコンで作ることを楽しんできました。
断片的なプログラムとは、「マップを描画するだけ」とか、「プレイヤーキャラを動かすだけ」とかです。
そういう憧れに向かうステップ(探求)に、心躍る喜びがありました。 - 創造性:
この創造性とはアイデアを形にする喜びのことです。
もともと自分のアイデアを形にする「ペーパークラフト」や「木工」などのモノ作りが好きだったので、プログラミングとの相性が良かったようです。
憧れに向かう、形にするのが楽しくて好きだ。そんなわけで、この個人ページではプログラミングの話をすることが多いです。
ここの管理人、
AI の利用やめるってよ。
AI の問題点:
- 自分で考えずに AI を利用することで、考える力が減退する。
- 人と人との交流(教える、教わる)が減る。
- 創作物のオリジナリティが無くなる。(自分の力で作ることの喜びが減る)
- 犯罪に使われている。
- AI のハルシネーション(幻覚を見ながら語ることがある)により、人間が間違った知識を AI から学んでしまう。
- 公序良俗に反するコンテンツの氾濫。(2025/10/18追加 ChatGPT の OpenAI がそのような方針をとったから)
これらが向こう10年解決されないだろうと見込んで、やめることにしました。(2025年5月23日~)
私は AI に頼らず「自分の力」を大切にしたいです。
…とはいえ、人間は新しく見つけた技術を手放すということは基本的にやらないと思います。
だから私も後々 AI を利用することにはなると思います。
でも上記の問題点は確かなもので、将来 AI ロボが私の家の扉をコンコンと叩いて
「市からの要請で、お手伝いするため おうかがいしました」
と言うまでの間は、この AI 技術を導入せず、頑張ってみようと思います。
でもこの考え方、キツイと思うのでマネしなくていいです。
- Special Documents -
特別な記事へのリンク
ゲームコーナー
その他 単発のアプリ
- 以降は日記です -

2026年3月1日
プログラミング 人体描画システム3
- 人体描画システムを知恵袋で活用し始めた
- 吹き出しのしくみ
- VBA 矢印図形の注意点
- しかし知恵袋の衰退
1. 人体描画システムを知恵袋で活用し始めた
私が今かかりきりで作っている「人体描画システム」。
知恵袋の回答の添付画像でさっそく使い始めましたね。
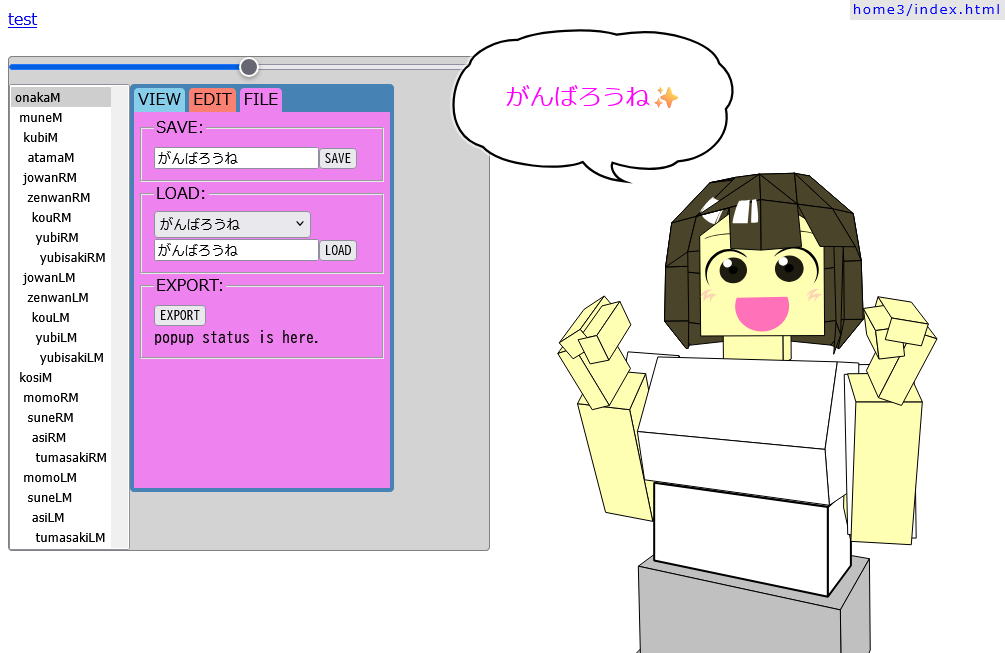
SAVE/LOAD 機能でポーズを呼び出すと、吹き出しはそのままにポーズだけが変わりますね。
たとえばこう、
▼寝ながらめんどくさそうに。
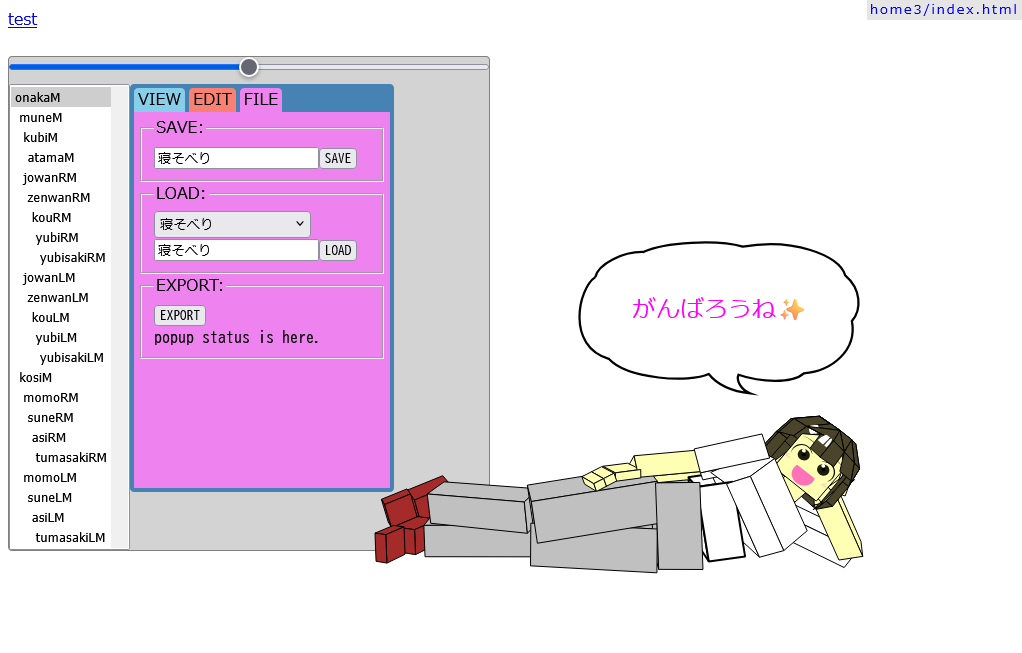
知恵袋の質問者たちを見ていると、こういう気楽なスタイルの方が良いのかもしれません。
▼やれやれポーズなのに言葉が逆。
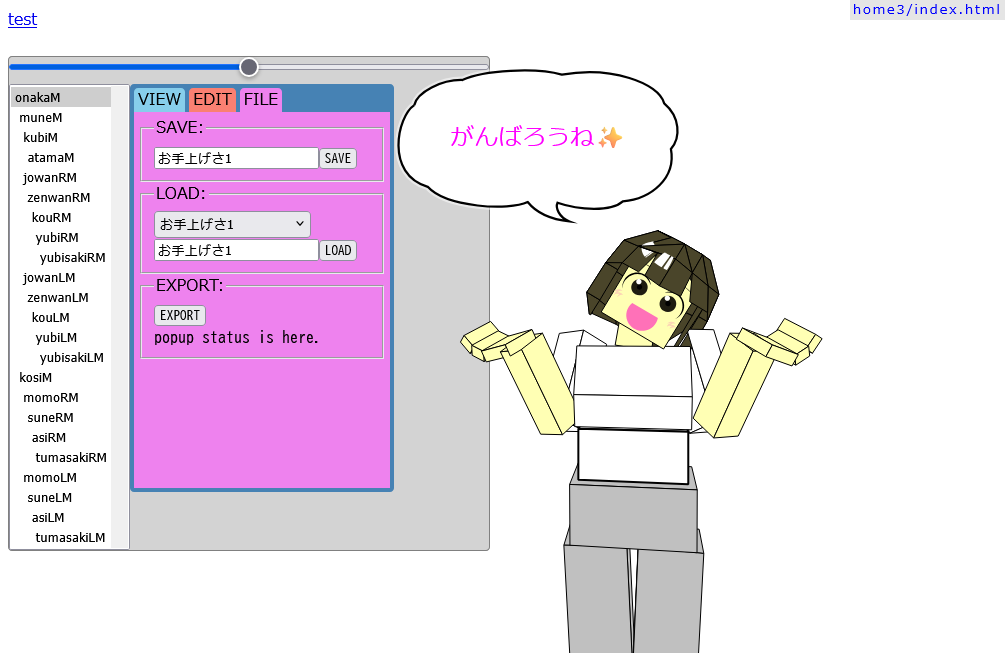
いるんだよなぁ、こういう回答者。頑張ろうとも言わずに。┐(´∀`)┌ヤレヤレ
▼お願いポーズで言われると…
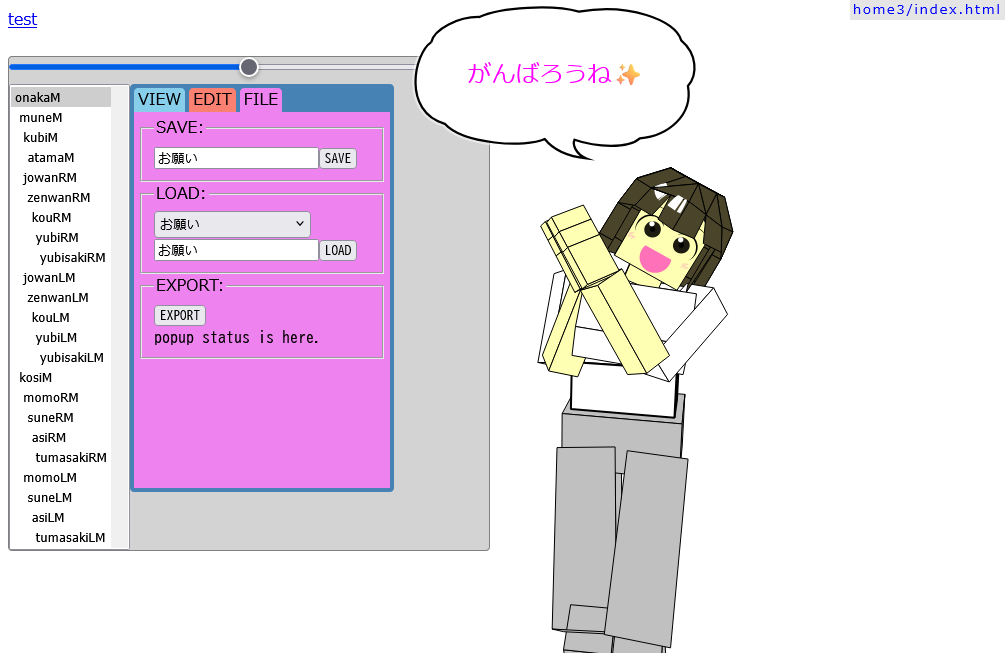
こういう感じのシングルマザーとかたくさんいそうだな。
2. 吹き出しのしくみ
以上、どのようなポーズに切り替えても、吹き出しは自然な位置を保っています。
吹き出しのデータは Excel で作っていて、そのときに、点線の四角形は「HTML で文字を表示する部分」を示しており、
赤い矢印が「吹き出しの "尾"(話者に向けられた尾状の印)の方向」を示しています。

Excel の図は、Excel VBA で操作することが可能で、点線の領域の位置とサイズ、矢印の位置と方向などをテキストファイルに落とすことができます。(図形自体は .png へ落とすメソッドがあります。私が使っている Excel 2010 では図を一度グラフの枠に入れて、グラフの枠に .png へ落とすメソッドがあるのでそれを利用します。最新の Excel ではたぶんグラフでなくても標準で .png へ落とすメソッドがあるんじゃないかと思います)
- テキストファイルに落とすときに、ファイル名を .js にして、内容を JavaScript にすれば、インターネットのページで使う JavaScript とすることができ、
- キャラの口の位置(実際やっているのは頭の中心です)の 3 次元座標を 2 次元座標へ投影し、
- 吹き出しの矢印の延長線上にその 2 次元座標が来るように、吹き出しの位置を調整すれば、吹き出しは自然な位置を保つことができる、
というしくみになっています。
3. VBA 矢印図形の注意点
しかし、Excel の図形で「直線の矢印」を作り、それを VBA で内部データを見ると、矢印の方向を示すデータは見当たりません。矢印の矢がどっちを向いているのか分からないと困ります。
なぜ方向データが無いのかというと、、

このような矢印を、
上下反転すれば、

左右反転すれば、

上限反転+左右反転すれば

…のようにすべて表現可能です。
だから「左上の開始点」と「矩形のサイズ」で直線の形を表現し、そして「上下反転する/しない」、「左右反転する/しない」というデータで「線の方向」を示しています。
だから矢印の方向を示すデータはないんです。
この説明をここに書かないと、私の記事を読んで「VBA で直線データを使おう」と思った人が、いざやってみると分からなくて困る、、ということになるので書いておきました。
4. しかし知恵袋の衰退
3D キャラ画像を知恵袋で活用し始めた、という話をしましたが、アメリカの「プログラミング知恵袋」である「Stack Overflow」は
下図グラフの左端が 2008 年 同サイト発足、
>Jeff Atwood and Joel Spolsky launched Stack Overflow for the public in 2008 as a programming Q&A website.
(ジェフ・アトウッドとジョエル・スポルスキーは、2008 年にプログラミングに関する Q&A ウェブサイトとして Stack Overflow を一般公開しました。)
ピーク時には 20 万件の質問を受付けていましたが、2022 年 11 月に ChatGPT が公開され、放物線を描くような落ち方を見せて、その後は斜め 45 度の降下が続き、グラフ右端の 2026 年では言葉通り「雀の涙ほど」となっています。
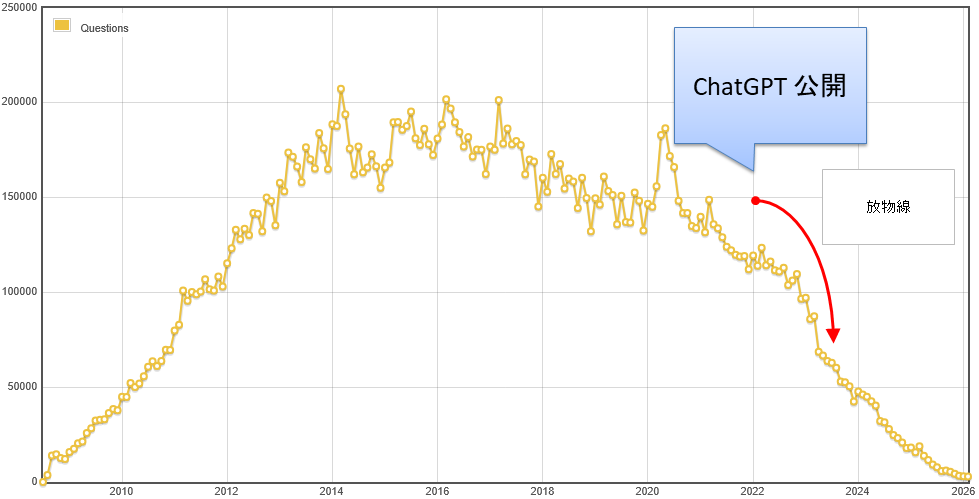
これが日本の「Yahoo!知恵袋」でも同様だとすれば、「知恵袋、知恵袋」と話題にするのも、なんだか時代遅れという感じもします。残念ですね。。
- 初心者に厳しい、
- 重複する質問が多すぎる、
- うかつなことを言うと叱責や罵倒が飛んでくる
(下記窓の杜の記事より)
という文化が知恵袋には多かれ少なかれあるので、それが ChatGPT 以前の若干の降下原因のひとつと言われています。
私のように「頑張ろう」みたいなメッセージを出す人は少数派ということですかね。
このグラフはここ、
https://data.stackexchange.com/stackoverflow/query/1926661
にアクセスして、「Run Query」ボタンを押し、「ロボットではありません」の認証を行って、再度「Run Query」ボタンを押して、「Graph」タブをクリックすることで誰でも表示できます。
↑この私が書いた「グラフ表示方法の案内」を、AI が人間に代わってできるかどうか試したら、まぁ多少の操作の差異はあるものの、AI の案内通りにやってみたら普通にグラフにたどり着けましたね。
もはや「波」といえるほどの AI 波(えーあい・なみ)が人間社会に押し寄せていて、人間の仕事がなくなる勢いですね。
こうやって記事を書く意味もなくなっていくのかなぁ。
「人体描画システム」でプログラミングを教えようとしているんですけど、、
AI や他の人にはできない私なりの教え方がたぶんあると思うので、その線でやってみるか…
「Stack Overflow」について報じた各ニュース
| 窓の杜: | 2026年1月9日 |
| IT開発者向けの質疑応答(QA)サイト「Stack Overflow」で投稿数が激減、ユーザー戦慄 | |
| GigaZine: | 2023年7月27日 |
| IT技術系Q&Aコミュニティ「Stack Overflow」のトラフィックがわずか1年半で半減、チャットAIによる影響か? | |
(訪問者のどんなニーズと この記事がつながるか)
- キャラに追従する吹き出しのしくみ
- 面白いものを見たい
- 日記を読みたい
2026年3月2日
プログラミング PC DOS J6.1/V + Turbo C
古い道具を使って、画面に円を描きましょう。
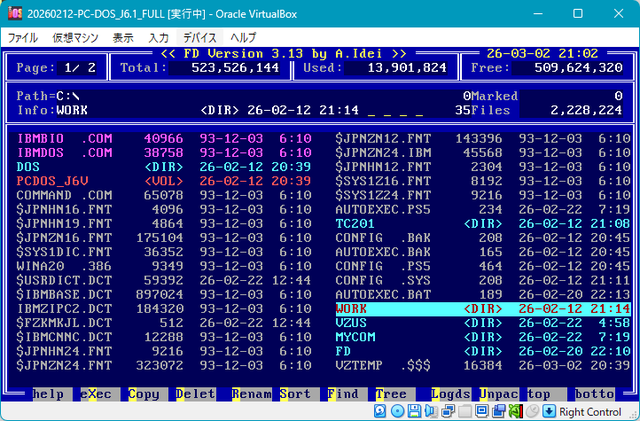
エミュレータの「VirtualBox」で PC DOS を起動して、ファイラーの FD を起動します。
Windows のエクスプローラーに相当するものです。
WORK ディレクトリに移動して、作業を始めます。
●
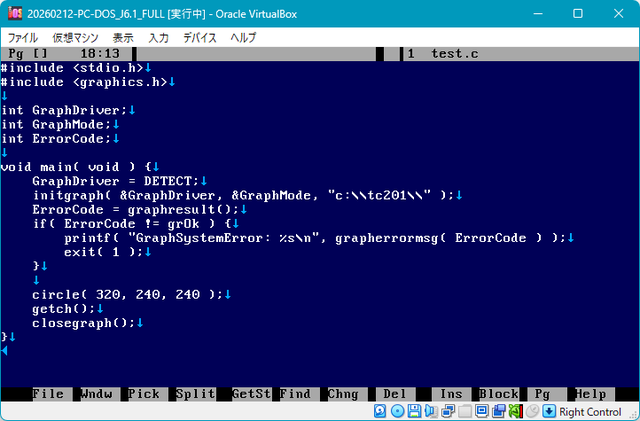
テキストエディタの「Vzエディタ」を起動しました。
PC DOS J6.1/V が英語モードなので Vz エディタも英語版が起動します。DOS が日本語モードなら Vz も日本語版。
FD も同じで、英語版と日本語版があります。
Vz エディタは最近オープンソースになりましたね。
そして、Turbo C に同梱の BGIDEMO.c を参考にグラフィック関係の設定を書き、
最後に circle( 320, 240, 240 );
と書く。
closegraph(); を最後に書かないと、実行後に画面が乱れてフリーズしました。これも BGIDEMO.c を見て学びました。
●
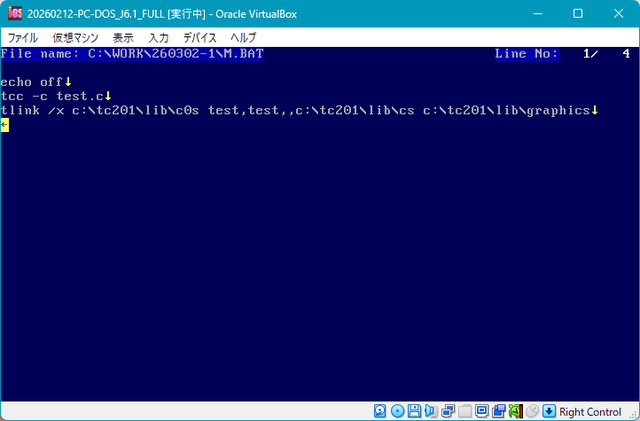
tcc -c test.c
というコマンドでコンパイルします。
tcc は「Turbo C のコンパイラ」という意味で tcc。
-c は「コンパイルだけして、実行ファイルは作らなくてよい」という意味です。test.exe ではなく test.obj が作られます。
そして、
tlink /x c:\tc201\lib\c0s test,test,,c:\tc201\lib\cs c:\tc201/lib\graphics
というコマンドで .exe の実行ファイルを作ります。
tlink は「Turbo C のリンカ」という意味で、tlink。
リンカは別々のファイルに収められたコンパイル済み関数群を1つのファイルへ結合するという道具なんですね。これがあるから .exe を作ることができます。
/x は「マップファイルを作らなくてよい」という意味です。
tlink を使うと map ファイルというものが作られますが使い方は知らなくて、いらないので作りません。
次の c:\tc201\lib\c0s は .obj の拡張子が省略されており、「C言語のゼロ」、つまり実行ファイルが実行を行うのに必要な「スタートアップ」のプログラムが書かれた部分、つづく s はメモリの使い方が「small」な方式です、という意味です。
続く test はこれも .obj の拡張子が省略されており、今回の円を描くプログラムをコンパイルしたもの。先に tcc で作った test.obj ファイルのことです。
,test,, の部分は実行ファイルの名前指定 test.exe のことで、
続く c:\tc201\lib\cs は .lib 拡張子が省略されており、メモリの使い方が「small」な方式、、のための各種関数をおさめたライブラリ。
最後の c:\tc201/lib\graphics はこれも .lib 拡張子が省略されており、今回のグラフィック関係の関数を収めたライブラリです。
これらを毎回コマンド画面に書くのは面倒なので、まとめて m.bat に書いて、
m と書いて Enter キーを押すだけでこれらのコマンドが実行され、test.exe ができる、という感じにしてあります。
m は make の m です。
●
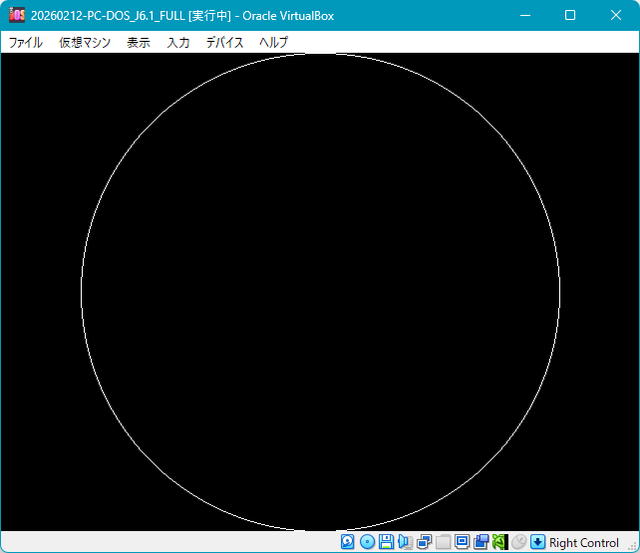
test.exe を実行すると、
きれいな円が描けました。
たのしすね。
でも最初、
tcc test.c
とだけやってエラー出していました。
できないから、後から、
c0s.obj とか必要なんだっけ、、と思い出したり、
「グラフィクス関係の関数が無い」というエラーが多発して、
えーーーっと??
と思って FD で探したら、graphics.lib があったので、これ付ければいいのか?と思って付けたら動いた、って感じです。
クールに最初から全部知ってるわけじゃないんですわ。
●
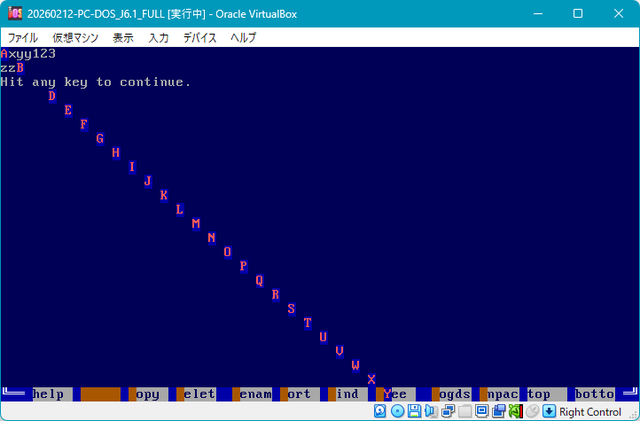
これは lasm(多摩ソフトの Light Macro Assembler)というアセンブラでテキスト画面をいじる関数を作って、そのアセンブリ関数を C 言語から呼び出す、ということを「どうやればいいのか」と思っていろいろ調べてやってみたものです。
●
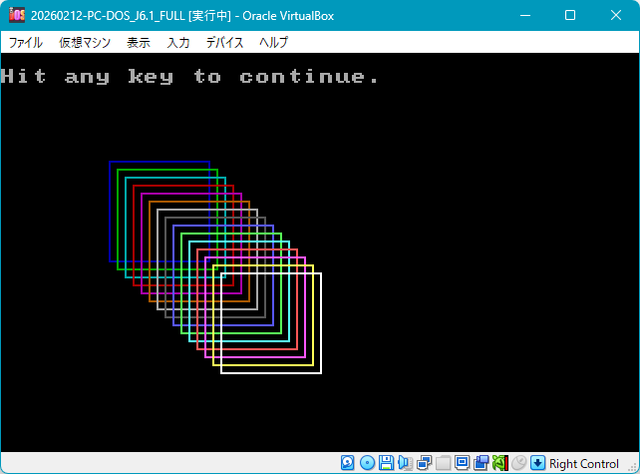
こちらはアセンブラでグラフィクスを描いたところです。
これをやりたかったのは中学生~高校生の頃で、
実際にできたのは 51 歳になってからの、つい先日のことです。
エミュレーター内ではあるけど、最速の超高速で描かれるわけですね。ここに可能性と宇宙とロマンがあります。
私がよく言う「プログラミングの宇宙」の起源は、メカニカルです。
VRAM や BIOS、ファンクションコールに、I/O など、メカ的な物が当時の古いコンピューターでは丸出しになっていて、ユーザーがいじって自由にあれこれできるんですね。
今の Windows はセキュリティでガチガチに固められていて、自由があるようで無い(宇宙が無い)んです。
以上は、PC DOS J6.1/V(有料)でなくても FreeDOS で、
lasm(有料)でなくても OpenWatcom の wasm で、
FreeDOS も wasm もフリーウェア、
FD はフリーウェア、Vz は有料だったけどオープンソースになった、
Turbo C ver 2.01(英語版のみ)もアンティークソフトとして無料公開これ(アンティークソフトのページは無くなったけどソフトウェアへの直リンクのみ (2026年3月2日現在) 生きています)、
…というわけで私がやったこれらのことは、全部無料で行えます。
(訪問者のどんなニーズと この記事がつながるか)
- プログラミングの話
- 懐かしいソフトウェアの話
- 日記を読みたい